The Z-Test

The z-test, like the binomial test, is a way of testing a hypothesis. It is not a very common form of hypothesis test because it requires us to have a great deal of information we do not usually have but it is an illustrative example that will serve as a stepping stone on the way to the t-test which has more practical applications.

In order to perform a z-test we need to know the the variance of the population that the sample is drawn from. This is not an easy thing to determine in practice.

Many IQ tests are tuned to produce a precise degree of variance when tested on the general population, one of the few somewhat real world examples of an instance where we can use a z-test. Imagine that we are using a test that is designed to have a standard deviation of 10 and a mean of 100. We give this test to 11 people who are supposed to be very clever. Their mean score is 107. The standard error should be:

se <- 10/sqrt(11)
se
 3.015113

Now that we know the standard error we can calculate the z-score in order to draw conclusions about the data we then determine. This is a form of normalization except we are adjusting for variability in the means rather than variability in the data itself. Thanks to the central limit theorem we believe that the mean values of a sample will follow a normal distribution.

z <- (107-100)/se
z
 2.321637

In a literal sense the z-score is how many standard errors from the population mean our sample mean is. This value is now compared to the standard normal distribution (also know as the z-distribution hence the name!) exactly the way we did with the binomial distribution.

1-pnorm(z)
 0.01012624

So there is about a 1% chance of getting a value as large or larger than the one we found and about a 2% chance of getting a value as extreme or more extreme. Generally we would be comfortable concluding that these people are, in fact, better at taking IQ tests than most people.

Central Limit Theorem – Again

A lot of decisions made in statistics rely on the central limit theorem. While the CLT is a bit abstract it is important enough that time should be taken to understand it. It goes like this:

The characteristics of independent samples from a population are approximately normally distributed.

It is important to note that this refers to the distribution of samples, not of the data itself (while many processes are normally distributed this is essentially a side effect of the above statement). This fact about samples is very useful because, as we saw when we looked briefly at the normal distribution, this means it is rare for sample values to dramatically from the population.

For example, the mean height of an American is about 162 centimeters. Even though there are three hundred million citizens it should be difficult to make a random sample of fifty people which has mean height of 100 centimeters.

What’s interesting and significant is that the CLT works with most distributions, you can estimate the mean even of strangely shaped data. Indeed this is so common that distributions that are exceptions, like the Cauchy distribution are considered “pathological”.

Before we continue let’s look at samples from a few different distributions.

# A population of ten thousand for the gamma, uniform, normal, and cauchy distributions.
gam <- rgamma(10000,1)
uni <- runif(10000)
nor <- rnorm(10000)
cau <- rcauchy(10000)

# The true mean of each population.
mg <- mean(gam)
mu <- mean(uni)
mn <- mean(nor)
mc <- mean(cau)

# We take a sample of fifty from each population one thousand times with a quick function.
samp.means <- function(x,rep=1000,n=50) {
	density(colMeans(replicate(1000,sample(x,n))))
}

pgam <- samp.means(gam)
puni <- samp.means(uni)
pnor <- samp.means(nor)
pcau <- samp.means(cau)

First we’ll visualize the shape of the distributions.

Now we visualize the shape of sample means, a vertical line shows the location of the true mean (the value we want to get).

For the first three the sample means stay close to the true mean even though they are very different in shape. For the Cauchy the samples have means that are all over the place, although the density happens to be highest near the true mean. Fortunately pathological distributions like the Cauchy are extremely rare in practice.

We talked about this before but we’re taking a second look at it again as part of a series that will lead to the t-test. There are actually a number of different central limit theorems. For example, one of the central limit theorems tells us that for normally distributed variables . . .

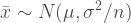
Which is to say that the sample mean, xbar, for a sample of size n, is distributed as a normal distribution with a mean of μ and a variance of σ² divided by the sample size. The Greek letters indicate characteristics of the population.

A formal proof of the behavior of samples from a normal distribution is available from PennState.

The fact that the central limit theorems are true is an extremely important result because they tell us a) that a sample will tend to be centered on the population mean and that b) it will tend to be relatively close. Moreover the

It is easy to demonstrate that the CLT is true but there is no immediately intuitive way to explain why the CLT is true. Nonetheless let’s use R to see this occur visually by looking at two trivial cases.

First imagine what happens with a sample of 1. The result of many samples will just be that we draw an identical distribution, one point at a time.

Now if we consider a taking a sample of 2 it is less obvious what will happen but we can write some code for an animation that will give us some idea.

x <- NULL
for(i in 1:50) {
	r <- rnorm(2)
	x[i] <- mean(r)
	h <- hist(x,plot=F,
		breaks=seq(-4,4,.25))
	
	comb <- seq(-4,4,.1)
	ncur <- dnorm(comb)

	title <- paste0('image',i,'.svg')
	svg(title)
	par(mfrow=c(2,1))
	plot(ncur~comb,type='l',xlab='')
	points(dnorm(r)~r,col='red')
	plot(h$counts~h$mids,type='h',
		xlim=c(-4,4),ylim=c(0,10),
		xlab='Mean',ylab='Count',
		lwd=3,col='red')
	dev.off()
}

We choose two values, compute the mean, and record it. Then repeat that process many times to slowly build up a distribution of means.