The Poission Distribution

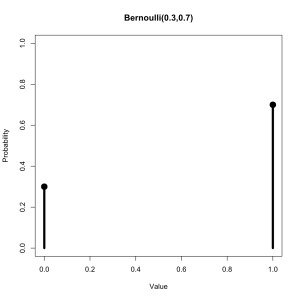
The Poisson Distribution

The Poisson distribution is actually based on a relatively simple line of thought. How many times can an event occur in a certain period?

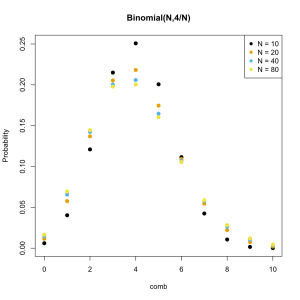
Let’s say that on an average day the help center gets 4 calls. Sometimes more and sometimes less. At any given moment we can either get a call or not get a call. This tells us that the probability distribution which describes how many calls we are likely to get each day is Binomial. Furthermore we know that it must be of the form Binomial(N,4/N) where where N is the greatest possible number of calls because this is the only way for the mean to be 4.

The question now becomes how many call is it possible to get in a day? Hard to say but presumably the phone could be ringing off the hook constantly. Its outrageously unlikely for me to get a hundred calls in a day but there is some probability that everyone in the building could need help on the same day. It is rarely possible to set an upper limit with confidence but watch what happens as we make the limit higher and higher.

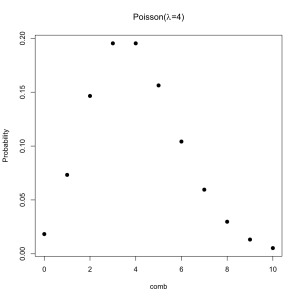
As we increase the The distribution is converging on a particular shape. Poisson proved what the shape would become if N were infinite. He also showed that this new distribution was much easier to calculate the form of than the Binomial distribution. Since a very large N and an infinite N are nearly identical the difference is irrelevant so long as its possible for the event to happen a large number of times.

Since the Poisson distribution is effectively a Binomial distribution with N always set to the same value we can describe the Poisson using only the average rate. Here it is for an average rate of 4 events per interval (calls per day, meteor strikes per year, etc).

It is occasionally said the the Poisson distribution is the “law of rare events” which is a sort of true but mostly confusing title. What matters is that the event could potentially happen much more often than it does.

A switchboard that gets an average of 100 calls an hour is not getting calls “rarely” but it is going to follow a Poisson distribution because a call can happen at any moment during the hour. If the switchboard were very slow and could only handle one call every ten seconds (so never more than 360 calls in an hour) it would be better to use a binomial distribution.

When explaining things it is often better to show than tell. Let’s look at an example of how the Poisson arises.

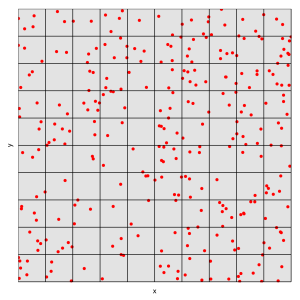
The Blitz was a massive bombing of Britain during World War II. A major concern of the British government was whether or not the Nazi bombs were precise weapons. If the bombs were guided their policies to protect people in the cities would have to be different. The analysts knew that if the bombing were random the distribution of bombs would have to follow an approximately Poisson distribution.

We can simulate a bombing campaign pretty easily by creating a large number of random coordinates to represent for each hit. The city is ten kilometers by ten kilometers.

set.seed(10201)
x <- runif(300,0,10)
y <- runif(300,0,10)
xy <- data.frame(x,y)

And what does this attack look like? We’ll plot each point and overlay a 10×10 grid.

p <- ggplot(xy,aes(x=x,y=y))
p + geom_point(size=2.5,color='red') +
	geom_hline(yintercept=0:10) +
	geom_vline(xintercept=0:10) +
	scale_x_continuous(minor_breaks=NULL,breaks=NULL) +
	scale_y_continuous(minor_breaks=NULL,breaks=NULL) +
	coord_cartesian(xlim=c(0,10),ylim=c(0,10))

During the Blitz each square had to be counted up by hand. We can do a little better. The cut() function divides up the data into one hundred sections then we rename them into something easier to read.

xx <- cut(x,10)
yy <- cut(y,10)
levels(xx) <- 1:10
levels(yy) <- 1:10

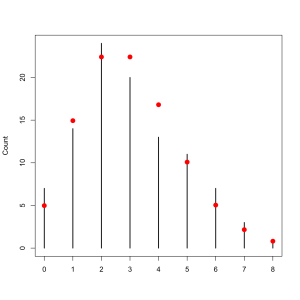
A contingency table tells now tells us how many bombs landed in each square. As a dataframe its easier to work with. Making a plot to see how often each number of its came up is then very simple.

fr <- data.frame(table(xx,yy))
plot(table(fr$Freq))

It isn’t a perfect, fit, of course, but as we discussed about the philosophy of statistics we do not expect perfection. The trend is one that clearly approximates the Poisson distribution.

Bernoulli Distribution

The Bernoulli Distribution

When we first started looking at statistical inference a few weeks ago the binomial distribution was introduced, which reflects the behavior of a coin that has been flipped many times. The Bernoulli distribution is simpler case which the binomial is a generalization of, it represent a coin flipped a single time.

Here’s an example for a biased coin:

bern <- data.frame(Value=c(0,1),Probability=c(.3,.7))

plot(bern,type='h',lwd=5,ylim=c(0,1),main="Bernoulli(0.3,0.7)")
points(bern,cex=2,pch=16) # Add large, solid color points

Obviously you can’t get a lot of mileage out of this distribution. It is, however, the source of a lot of common terminology in statistics. By tradition Heads = 1 and Tails = 0 (which part of the reason that in R and many other languages the logical values TRUE and FALSE equal 1 and 0, respectively). The probability of Heads is written p while the probability of tails is written q. Since a coin only has two sides it is always true that q = 1-p and p = 1-q.

Anything that has discrete “success” and “failure” modes can be considered a Bernoulli trial. Flipping a coin is a Bernoulli trial. Rolling a die is a Bernoulli trial if you define every face as either success of failure (ie “a 6 is a success” or “all odds are successes”). Some things are close enough to Bernoulli trial that they can generally be thought of in these terms, for example, many text books use the sex of a newborn as a an example of a Bernoulli trial even though about 1% of people are born with ambiguous or intersex characteristics.

Bernoulli’s name is also given to the concept of a Bernoulli process which is multiple, independent, identical Bernoulli trials. This means that this is more than one trial, trials have no effect on each other, and the probability of success is the same each time. This is what creates a binomial distribution (flipping a coin many times). On the other hand drawing black and white marbles from a box isn’t a Bernoulli process because once you take a black marble out the probability of drawing a black marble decreases, the trials are not identical.

Multiple Comparisons

Frequentist methods of inference require experimenters (and reviewers) to guard against multiple comparisons. The problem is as follows: Each test is designed to avoid give false positives only at a certain rate but this means that when many tests are used false positives become progressively more likely. Indeed presence of false positives when the critical p-value is 0.05 should follow a Binomial(0.05, N) distribution where N is the number of comparisons.

As a result either a correction is applied or a more appropriate test is used. The simplest correction is called the Bonferroni and simply means dividing the critical value by the number of comparisons.

The Bonferroni correction is, in my opinion, something of an admission of defeat on the part of the experimenter. There is usually an appropriate generalization for a given test. For example the ANOVA is a generalized t-test and the MANOVA is a generalized ANOVA. Devising a new method to deal with a complex procedure is rarely practical. Strictly speaking the Bonferroni isn’t inappropriate (although it is conservative) but when you see it that’s generally an indication that someone looked at their experiment and realized they didn’t have the statistical tools to analyze it.

A further danger of the multiple comparisons problem is that mining for p-values (sometimes called p-hacking) is basically impossible to guard against. Even if an experiment reports only a few comparisons there’s no way of knowing how many comparisons were made and discarded before the experimenter chose to report those ones. This is a serious problem. Evidence of p-hacking has been found in several fields simply by analyzing the distributions of reported p-values and looking for a “bump” near a popular critical value.

Interestingly there is no correction made for multiple comparisons in Bayesian analysis. To someone familiar with traditional p-value based tests this seems immediately absurd and suspicious. Nothing about Bayesianism seems to guard against false positives! Recall, however, that the difference in methods is caused by a difference in core philosophy. There is no such thing as a false positive in Bayesian analysis so it makes no sense to try and prevent them. The knowledge implied by the data is what it is, regardless of how many comparisons are made. The Bayesian tests have no discrete “positive” or “negative” results.

This isn’t to say that Bayesian tests can’t be manipulated but doing so often means making an explicit change to the model. For example you could assume a very informative prior but since you have to define your model at some point doing so is obvious to the reader. Gelman and Hill (2006) suggest that when constructing a hierarchical model one should feel free to try multiple models. This does open up the analysis to manipulation and the only safeguard I’m familiar with is to apply model checking techniques to ensure that the model is not an absurd one. From the position of Bayesian philosophy, though, none of the models are wrong and it is job of the reader to decide if they are acceptable.

Next week I’ll be teeming with a lot of news about the binomial distribution and its extended family.

Weird Facts from MTG JSON: First Letters

A short little post today that will hopefully be part of an intermittent series. We’ll interrogating the JSON file we extracted a while back.

The question we want to answer today is: What is the most common first letter in the names of cards? Naively we might think that they’re all close to equally common and with a bit more thought we’d realize that certain letters like Q, X, Y, and Z are liable to be much less common than others.

First lets extract the name of every card that isn’t from a joke set (called the Un-sets).

a <- AllCards[AllCards$exp.type != "un",]$name

Some cards get reprinted multiple times and, while this probably wouldn’t throw off our results too dramatically much we should get rid of those repeated names in the interest of fairness. The unique() function does that for us.

names <- unique(a)

How to get the first letter from each name, though? For that we have to return to the regex capabilities that R has. There is a large family of function for working with strings of text. The substring() function asks us to provide it a vector (we have one of those!) then tell it where to start reading (the first letter) and where to stop reading (also the first letter).

letters <- substring(names,1,1)

Just like that we’ve got a vector of first letters for every unique name. To count up how many of each we just use the familiar table() function.

table(letters)
letters
   Æ    A    B    C    D    E    F    G    H    I 
  28  748  799 1000  827  485  636  785  504  340 
   J    K    L    M    N    O    P    Q    R    S 
 148  403  441  901  346  277  724   55  775 1993 
   T    U    V    W    X    Y    Z 
 852  169  388  542   14   51   77

barplot(table(letters),ylim=c(0,2000),
	main="First Letter of Magic Cards")

The letter S is outrageously popular, thanks in large part to names that start with “Sky”, “Soul”, “Sword”, and “Sylvan”. I think its more interesting that the rarely used letter Æ (pronounced ‘ash’) is twice as popular as X. There is an editorial policy where the word “aether” is always rendered as Æther, so it shows up on a number of cards that refer to ephemeral magic.

This also makes it easy determine how many unique Magic card have ever been printed:

length(names)
14308

It’s actually a bit less than that because there are twelve token cards included in the data and thirty three double faced cards, for which each side is counted.

Often, Frequently, Only Once

There are two major competing schools of thought in modern statistics, divided most obviously by methodology. The underlying difference, however, can be considered one of philosophy.

The traditional school of thought (sometimes called Frequentism) holds that there are basic truths about the universe (the force of gravity, the average height of everyone on the planet) which we attempt to learn. Statistics, in this view, is how we make up for the imperfections in our own knowledge about the universe. In Frequentism data is variable.

The alternative school, Bayesianism, hold that it is simply impossible to know the truth and thus our goal can never to be to determine if we are “right” or “wrong” about our conclusions. Because of this the role of Bayesian statistics is to shape our knowledge or beliefs in accordance with the data. In Bayesianism the truth is variable.

This difference in philosophy continues to the description of errors.

Frequentism has Type I and Type II errors which are false positives and false negatives respectively. These types of error reflect the fact that the goal of Frequentist testing is to avoid getting the wrong answer. Frequentist tests use p-values to evaluate the results.

Bayesianism has Type S and Type M errors which are incorrect sign and incorrect magnitude respectively. An appropriate Bayesian test cannot be wrong because that is meaningless in a Bayesian context, it will correctly describe our knowledge. The errors reflect the fact that the goal of Bayesian testing to come close to the population value. Bayesian tests use distributions of credible values to evaluate results.

Let’s look at our examples of traditional and Bayesian binomial tests to see this difference. Here we will download Rasmus Baath’s bayes.binom.test() function.

set.seed(1771) # Use this function to get the same pseudo-random numbers that I do.

## Simulate flipping a coin twenty times and count up the heads.
total <- 20
flips <- sample(c(0,1),total,replace=TRUE)
heads <- sum(flips)

mod.freq <- binom.test(heads,total) # Frequentists
mod.bayes <- bayes.binom.test(heads,total) # Bayesian

mod.freq
        Exact binomial test

data:  heads and total
number of successes = 9, number of trials = 20, p-value = 0.8238
alternative hypothesis: true probability of success is not equal to 0.5
95 percent confidence interval:
 0.2305779 0.6847219
sample estimates:
probability of success 
                  0.45 

mod.bayes
        Bayesian First Aid binomial test

data: heads and total
number of successes = 9, number of trials = 20
Estimated relative frequency of success:
  0.45 
95% credible interval:
  0.26 0.66 
The relative frequency of success is more than 0.5 by a probability of 0.333 
and less than 0.5 by a probability of 0.667 

The traditional test tells us that if we performed an identical test many times we would up with a result like this about 82% of the time and so we should not believe that the coin is unfair. With a critical value of 0.05 we expect that we will only mistakenly call the coin unfair 5% of the time.
The Bayesian test tells us that based on what we have seen the credible values of the coin’s fairness includes 0.5 but it is somewhat more likely that the coin is biased low.

As we saw two weeks ago these are very different pieces of information, even though they come from identical data and both are true. I would argue that the Bayesian result is a much more useful piece of information but that is discussion we’ll come back to at later date.

On Friday we will take a look at corrections for multiple comparisons.

Philosophy of Statistics

The early history of statistics can be credited to essentially two groups: Demographers and later actuaries who needed information about populations (hence having the same root as state) and gamblers who wished to make better bets. The interest in statistics as a method of formal inference, as scientists use it today, was a much later development. Before various theories of errors, such as the Central Limit Theorem, existed problems of inference about anything other than very simple events were nearly impossible. Today statistics is used in science, engineering, business, in countless ways. When people wish to describe and predict the world around them with precision they apply statistics.

What does this make statistics as a philosophy? As a field it is the practice of working with data. To think of it as a philosophical position it is good practice to try to determine the guiding principle of the field.

For instance physics has the “cosmological principle” which states that the laws of nature are the same in every place and every time. This is a core belief of the field and arguably the only necessary one. Without it no one could make any sort of statement about physics, generalization would be impossible.

Statistics has no such widely recognized basic principle. Andrew Gelman has suggested in passing the a statistician should be a person who thinks in continuous terms rather discrete terms. I would suggest the simple statement that “Empirical measurements are only ever probabilistic.” as something that nearly all statisticians would agree upon.

Like the cosmological principle this is very simple on the surface but has a large impact on how one looks at the world. In 1722 Roger Cotes made the observation in an appendix to his book Harmonia mensurarum, titled Aestimatio errorum, that possessing more data allows for a more accurate conclusion about things. This was soon generalized so that by the end of the century it was accepted that many careful measurements were better than a single supposedly perfect measurement.

This way of thinking, and its formal mathematical consequences, have continued to shape the nature of science into the modern day. Even though the cosmological principle tells us that the speed of light is a constant it is not a problem that Michaelson’s rotating mirror experiment determined a different value for the speed of light each time it was run.

The interpretation of what it means that measurements are probabilistic is currently at the center of a debate in modern science. In our next post we will look at that rift between the methods and philosophies of Frequentism and Bayesianism.

Webscraping Images

Now let’s webscrape some images from mtgimage.com to see how we can work with images in R itself. We will need the RCurl and jpeg packages installed and loaded in order to do this. RCurl will give us some webscraping functions while jpeg allows R to convert .jpegs image files into a form R can read.

install.packages('RCurl')
library(RCurl)
install.packages('jpeg')
library(jpeg)

By using regular expressions we’ll look at just the creatures with the Beast subtype from our extracted JSON file, and get their ID codes.

codes <- MRD[grep("Beast", MRD$subtype),]$ID
codes
 "48436" "46556" "46123" "48603" "46115" "48600" "48083"

Since mtgimage.com is designed to be as easy to reference it is trivial to use this information to create a bunch of URLs that we will reference later. The paste() function to drop each multiverse ID into the middle of some text. The only thing we have to do is tell it that the separator value will be nothing (by default it is a space).

Once we have that

urls <- paste("http://mtgimage.com/multiverseid/",codes,"-crop.jpg", sep="")

jpglist <- list()
for (i in 1:7) {
	jpglist[[i]] <- readJPEG(getURLContent(urls[i]))
}

Now we have a bunch of raster files (ie bitmaps) and the built in rasterImage() function to visualize them with. The simplest way to show them is to call a new plot and put the image on it.

plot.new()
rasterImage(jpglist[[1]],0,0,1,1)

Why would you want to do this with R?

To be perfectly honest it isn’t something that is called for often with statistical software but it is a great chance to get practice with how things are referenced in R.

Extracting from a JSON File

In our last post we learned about how to deconstruct unfamiliar data in order to get a idea of what information is in it. Extracting the data into a workable form is the next step. Fortunately I’ve written a function to do exactly that. The annotations are contained in the code.

# Converts an extracted section of AllSets.json into a dataframe. Input should
# be in the form of AllSets$[Set Code].

extract.cards <- function(x) {
	
	# Grab the set code, block name, and the type of set.
	code <- x$code
	exp <- x$type
	if(class(x$block) == "NULL") {
		blk <- "NA"
	} else 
	blk <- x$block

	# Now we switch to just the cards.
	x <- x$cards
	
	# Create empty vectors of the correct size
	# of values for quicker loops later on.
	len <-rep("",length(x))
	type <- len
	subtype <- len
	name <- len
	cmc <- len
	pwr <- len
	tns <- len
	rare <- len
	color <- len
	ID <- len
	layout <- len

	## Each card in a given set has the same set code, 
	## block name, and expansion type. We just repeat
	## the value many times.
	set <- rep(code,length(x))
	block <- rep(blk,length(x))
	exp.type <- rep(exp,length(x))

	# A big loop wherein we extract information from each card.
	for(i in 1:length(x)) {
		card <- x[[i]]

		# Every card has exactly one rarity and exactly one name. The
		# layout type will let us filter certain unusual card types.
		name[i] <- card$name
		rare[i] <- card$rarity
		layout[i] <- card$layout
	
		# Slightly harder. Cards can have several types, subtypes, 
		# and colors. We use paste() to collapse together these
		# multiple values.
		type[i] <- paste(card$types[1:length(card$types)],collapse=" ")
		subtype[i] <- paste(card$subtypes[1:length(card$subtypes)],collapse=" ")
		color[i] <- paste(card$colors[1:length(card$colors)],collapse=" ")

		# Most complicated. These values can sometimes be blank.
		## ID (a few promotional cards lack ID codes)
		if(class(card$multiverseid) == "NULL") {
			ID[i] <- "NA"
		} else
		ID[i] <- card$multiverseid

		## Total Cost
		## Cards without a listed CMC actually have a value of
		## zero.
		if(class(card$cmc) == "NULL") {
			cmc[i] <- 0
		} else
		cmc[i] <- card$cmc

		## Power and Toughness
		if(class(card$power) == "NULL") {
			pwr[i] <- "NA"
		} else

		pwr[i] <- card$power

		if(class(card$toughness) == "NULL") {
			tns[i] <- "NA"
		} else
		tns[i] <- card$toughness
	} # End of the loop!

	## Clean up work so we can read stuff more easily! ##

	# Make power, toughness, and cmc into numerics. This will make a few
	# things into NAs but that's okay.
	pwr <- as.numeric(pwr)
	tns <- as.numeric(tns)
	cmc <- as.numeric(cmc)
	
	# Convert a few things to factors to save space.
	rare <- as.factor(rare)
	type <- as.factor(type)
	subtype <- as.factor(subtype)
	set <- as.factor(set)
	block <- as.factor(block)
	exp.type <- as.factor(exp.type)
	layout <- as.factor(layout)

	# Simplify the names for each color then convert to 
	# a factor and make empty values read as C for colorless.
	color <- gsub("White","W",color)
	color <- gsub("Blue","U",color)
	color <- gsub("Black","B",color)
	color <- gsub("Red","R",color)
	color <- gsub("Green","G",color)
	color <- as.factor(color)
	levels(color)[1] <- "C"

	# Everything goes into a dataframe.
	data.frame(
		name, ID, type, subtype, cmc, color, 
		power=pwr, toughness=tns, rare, set, 
		block, exp.type, layout,
		stringsAsFactors=F)
}

Code updated 8/2/2014 to add layout information.

Now lets grab all of the data from the MRD set and look at a random selection of cards.

MRD <- extract.cards(AllSets$MRD)

MRD[sample(nrow(MRD), 3), ]
                  name    ID        type subtype cmc color power toughness   rare set    block  exp.type
298 Wanderguard Sentry 48439    Creature   Drone   5     U     3         3 Common MRD Mirrodin expansion
203            Regress 49061     Instant           3     U    NA        NA Common MRD Mirrodin expansion
41   Contaminated Bond 49444 Enchantment    Aura   2     B    NA        NA Common MRD Mirrodin expansion

Where is the Fangren Hunter we met last time? Regular expressions let us search for a particular string. We combine that with the subsetting notation to track down a name.

MRD[grep("Fangren Hunter",MRD$name),]
             name    ID     type subtype cmc color power toughness  mana   rare set    block  exp.type
66 Fangren Hunter 46115 Creature   Beast   5     G     4         4 3 G G Common MRD Mirrodin expansion

Awesome! We’ve taken information in an unfamiliar format and turned it into a convenient dataframe. Obviously most JSON files don’t contain information about Magic cards but extraction is hardly difficult.

Next we’ll use webscraping to extract images from the internet and put them into a format that R can work with.

Working With JSON Files

I am a big fan of Magic: The Gathering and data regarding the game is my preferred way to experimenting with new techniques since I don’t know or care enough about baseball to look at that data. Thanks to Robert Shultz from mtgjson.com an up to date and easy to read file with information about Magic cards is readily available for us to check out.

This also gives us a chance of learn about how to deal with data in a foreign fomat.

The JSON format is a popular and incredibly lightweight way to store data. In R it can be read with the rjson package by Alex Couture-Beil. Once you’ve installed the rjson package and downloaded the AllSets.json file to your working directory we’ll load them into R.

library(rjson)
AllSets <- fromJSON(file="AllSets.json")

Notice that the JSON file loads in just a moment despite the fact that it describes more than twenty thousand objects, each with at least eleven characteristics. Much faster than reading a .csv file, for instance.

Exploring a foreign data format can be tricky. In particular we now have to deal with the fact that JSON files that are loaded into R become an unwieldy list of lists. There is no convenient way to summarize them. It is also very difficult to work with lists if you’re doing analysis or just searching for information. We would much prefer to have a dataframe. In fact the data here is so large and unfamiliar that we have to learn a new trick just to see what’s going on. If you just ask for the str() of the AllSets data you get more lines of data than R can show, not an improvement. Fortunately we can tell str() to not show every nested level of the data.

Here are the first few lines, showing just level 1.

str(AllSets, max.level=1)
List of 136
 $ LEA:List of 8
 $ LEB:List of 8
 $ ARN:List of 8

There are 136 sets included in the file (as of this post), from Limited Edition Alpha (1996) all the way through to Magic 2015 (2014). Each of them is referred to via a three letter code. If you read down the list a bit you’ll find a set abbreviated as MRD. Now let’s specify that we want to see the structure of MRD with that same safety valve to keep us from getting flooded with information.

str(AllSets$MRD, max.level=1)
List of 8
 $ name       : chr "Mirrodin"
 $ code       : chr "MRD"
 $ releaseDate: chr "2003-10-02"
 $ border     : chr "black"
 $ type       : chr "expansion"
 $ block      : chr "Mirrodin"
 $ booster    : chr [1:15] "rare" "uncommon" "uncommon" "uncommon" ...
 $ cards      :List of 306
  .. [list output truncated]

We can see a few easily understood things about it the set: It’s name is Mirrodin, there are 306 cards in it, and the set was released on February 10th 2003. Additionally the Mirrodin set is part of the Mirrodin block (the storyline that was covered that year). The remaining information is fairly technical but should make sense to anyone familiar with the game.

Let’s look at the 66th card of the set in a compact form. The unlist() function turns the list of characteristics into a named vector instead. Let’s also get rid of line 15 since it’s very large and not very important.

unlist(AllSets$MRD$cards[[66]][-15])
            layout               type              types             colors 
          "normal" "Creature — Beast"         "Creature"            "Green" 
      multiverseid               name           subtypes                cmc 
           "46115"   "Fangren Hunter"            "Beast"                "5" 
            rarity             artist              power          toughness 
          "Common"    "Darrell Riche"                "4"                "4" 
          manaCost               text             number          imageName 
       "{3}{G}{G}"          "Trample"              "119"   "fangren hunter" 

The card is the creature “Fangren Hunter”. Another site by Robert Shultz, mtgimage.com, provides us with an image of the card itself.

In our next post we’ll take a look at how to extract all this data from the JSON format into a dataframe. Exploring that will give us a chance to practice again with subsetting notation and regular expressions.

Hypothesis Testing – A Warning

Consider the traditional binomial test for a moment. The goal is to decide whether or not the sample we have is reasonable based on our hypothesis. This is called a significance test.

There is a problem with this, however, namely that there is no subtlety in the hypothesis. If we hypothesize that a coin is fair we mean that the coin has a probability of 0.5 of heads. This is fine in the realm of pure mathematics but in reality it is always true that the null hypothesis is wrong. No coin will actually be perfectly fair but it may be extremely close to fair, so much that it is irrelevant.

Imagine a coin that flips heads with a probability of 0.495, which is quite good. The binomial test doesn’t care, though. For a small sample of rolls the binomial test lacks the sensitivity to notice that 0.495 is not 0.5 but as the sample gets larger the test becomes more sensitive. Eventually it will begin to notice even meaningless differences and report that it is improbable the die is fair.

We can actually watch this happen with a bit of R code. We will keep the same relative probability of heads as we increase the sample.

h <- 495*c(1,2,5,10,20)  #Number of heads
t <- 1000*c(1,2,5,10,20) #Total sample size

a <- binom.test(h[1],t[1])
b <- binom.test(h[2],t[2])
c <- binom.test(h[3],t[3])
d <- binom.test(h[4],t[4])
e <- binom.test(h[5],t[5])

# Extract the p-values as a vector then print them out to three decimal places for ease of reading.
round(as.numeric(c(a[3],b[3],c[3],d[3],e[3])),3)
[1] 0.776 0.671 0.488 0.322 0.159

With a sample of 1000 we are told that there is a 77.6% chance of getting so extreme a value. With a sample of 20000, though, the chance is just 15.9%. This is a result of the test working correctly but perhaps not intuitively.

With a huge sample the test is very sensitive, it becomes better at discriminating between the null hypothesis and the alternative. What the test does not do (and is not meant to do) is tell us whether the difference is large or meaningful. By taking an arbitrarily large sample we can guarantee that the p-value of the test will be low, no matter how close the coin is to being fair.

Be careful when interpreting p-values and keep an awareness of what they are and are not!