The Circle – Sine and Cosine

In high school people are usually taught the three trigonometric functions, which is odd because there are a lot more than that, nine that see regular use. They can be thought of as three pairs of three starting with the sine, cosine, and tangent. It takes a bit of work to draw each of these functions so the code is presented at the end of the post rather than with each graphic.

Let’s draw a circle and use it to construct the values of the functions. All of them correspond to a characteristic of a triangle draw on the circle. Let’s start with the sine and cosine because they have the most natural representations.

Here are the sine and cosine:

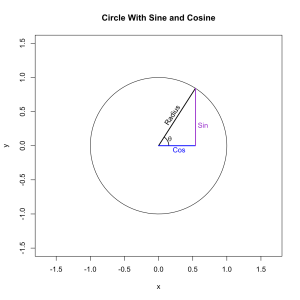
They have the length of those two colored lines respectively. The length of those lines is completely determined by the length of the radius and the angle of theta. In this case the angle is 1 radian and the radius of the unit circle is exactly equal to 1 so we can use R to find that . . .

sin(1)
[1] 0.841471
cos(1)
[1] 0.5403023

In other words the sine of theta gives us the y-coordinate of a point on the unit circle and the cosine of theta gives us the x-coordinate of that same point. Just by looking at the image we can intuit certain properties of the two functions. Both of them vary between -1 and 1, the bounds of the circle, and they’re offset by exactly 90 degrees (π/2 radians) which means that the sine of π is the same the cosine of π/2.

If we plot how the vales of the sin and cosine change with in inputs we get a pair of waves.

x <- seq(-5,5,.1)
y1 <- sin(x)
y2 <- cos(x)

plot(y1~x,
	main = 'Sine and Cosine Waves',
	lwd = 3, col = 'blue', type = 'l',
	ylim = c(-2,2))
lines(y2~x, lwd = 3, col = 'darkorchid')

These are are the shape that you see on oscilloscopes in old science fiction movies (or at work if you often measure voltages). You can see that there are points where the two curves cross at all of the multiples of π/4 (a 45 degree angle).

Notice that the three lines (radius, sine, and cosine) together describe a right triangle. Because of this the trigonometric functions can be used to solve triangles and then to solve much more complex structures because we can build them out of triangles. If we vary the radius of the circle the length of the other lines scale proportionally. In fact this is true for all of the trigonometric functions. As a result we can simply a lot of things by working on the unit circle and then scaling appropriately when we’re done.

Let’s use this fact to derive an important fact about the sine and cosine.

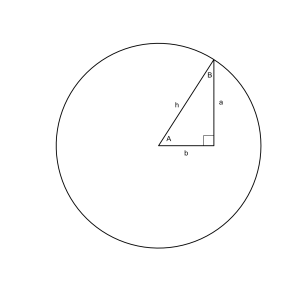
Using the sine, cosine, and tangent it is possible to fully describe a right triangle with just a few pieces of information. Consider a simple right triangle on a circle with angles of A = 1, B = 0.57, the third angle is π/2 since its a right angle.

The sine of angle A is 0.84 so we know that side a has a length of 0.84r and the cosine of A is 0.54 so we know that the length of side b is 0.54r, where r is the length of the hypotenuse (or the radius). This follows quite obviously from the definition of sine and cosine and the properties we’ve discussed. The only piece of information we don’t have is the length of the radius since we don’t know if this is a unit circle or not.

Can we calculate it?

Actually no, we cannot. There are an infinite number of valid triangles with those angles!

That’s unfortunate but considering what would happen if we knew that the length of side a is very illustrative. If the hypotenuse was exactly equal to 2 we knew that we could solve the entire triangle! Why? Consider again the value which we calculated which was 0.84r. That 0.84 is constant, only the r can vary as the size of the triangle increases or decreases.

In other words . . .

So if the angle A 1 and the length of the corresponding side is 2. . .

This is where the identities taught to school children as “sine equals opposite over hypotenuse” and “cosine equals adjacent over hypotenuse” come from. Intuitively if the length of the sides is determined by the hypotenuse and the angle then the angle must be determined by the hypotenuse and the sides!

Next up is the tangent function!

Code for drawing the sine and cosine. The circ() function is not from base R, we created last time.

circ(xlim = c(-1.5,1.5), ylim = c(-1.5,1.5), lwd = 1, 
	main = 'Unit Circle With Sine and Cosine')
segments(0, 0, cos(1), sin(1), lwd = 2)
text(.20, .45, 'Radius', srt = 57)
lines(th, lwd = 1.5)
text(.17, .1, expression(theta))
segments(0, 0, cos(1), 0, lwd = 2, col = 'blue')
text(.3, -.05, 'Cos', col = 'blue')
segments(cos(1), sin(1), cos(1), 0, lwd = 2,col = 'darkorchid')
text(.65, .3, 'Sin', col = 'darkorchid')

Drawing the triangle to solve. Basically the same shape with different labels.

segments(0, 0, cos(1), sin(1), lwd = 2)
segments(cos(1), sin(1), cos(1), 0, lwd = 2)
segments(0, 0, cos(1), 0, lwd = 2)

text(.1, 0.07, 'A')
text(cos(1)+.07, sin(1)/2, 'a')
text(cos(1)/2, -0.07, 'b')
text(cos(1)-.04, sin(1)-.15, 'B')
text(cos(1)/3, .4, 'h')

rect(cos(1)-.1,0,cos(1),.1)

ANOVA

An analysis of variance is a very common statistical test, although one which answers such a non-specific question that it can seem surprising that it is used at all. The null hypothesis which an ANOVA addresses is . . .

. . . “is the mean of every group the same?”

The alternative hypothesis is that at least one of the means is different.

It is called the analysis of variance because it compares within group variability to between group variability.

Like Ronald Fisher we will look at the iris data as an illustrative example. In this case we will use the petal lengths. Before we start let’s look at the output R gives us for an ANOVA of the data. As we examine the logic of the ANOVA we will come back to this output and see where each piece comes from.

options(show.signif.stars=F)
mod <- aov(iris$Petal.Length~iris$Species)
summary(mod)
              Df Sum Sq Mean Sq F value Pr(>F)
iris$Species   2  437.1  218.55    1180 <2e-16
Residuals    147   27.2    0.19

Okay now the logic step by step. The first thing to check should be if the means are generally close together.

The grand mean of the data is . . .

mean(iris$Petal.Length)
 3.758

. . . and the group means are . . .

with(iris, tapply(Petal.Length, Species, mean))
    setosa versicolor  virginica 
     1.462      4.260      5.552 

They’re not really clustered but surely this is the kind of thing which might occasionally occur by accident just due to natural variability. What we need from the ANOVA is a way to quantify this tendency.

In order to describe the between total variability we will compute the sum of squares . . .

sum.squares <- function(x) {
	a <- mean(x)
	b <- (a-x)^2
	out <- sum(b)
	out
}

You should recognize this process of taking the difference between the mean and each data point, squaring it, and summing the result as part of the calculation of the variance. The SS and variance are, in fact, near relatives. The SS is a way of looking at the variability. It happens that we can partition the SS in a way that we cannot do with the the raw differences so this will make our work easier in the future.

The total sum of squares . . .

tot.SS <- sum.squares(iris$Petal.Length)
round(tot.SS,3)
 464.325

. . . and we will do the same thing to find the within group sum of squares . . .

in.SS <- with(iris, tapply(Petal.Length, Species, sum.squares))
round(in.SS,3)
    setosa versicolor  virginica 
     1.478     10.820     14.925

We can see why Fisher chose this example, it is very good for an analysis of variance because the total SS of squares is obviously much larger than the within groups SS (and thus the between groups variance will be as well).

Adding up the SS within each group tells is the total within groups SS. Then we can subtract that from the total SS to see how much comes from differences between the groups.

round(sum(in.SS),3)
 27.223

between.SS <- tot.SS - sum(in.SS)
round(between.SS,3)
 437.103

So far everything we’ve done should be easy to follow, we’re just computing the SS and then cutting it up into pieces (something we can only do with the SS). Nonetheless, it might be easier to follow as a table.

Compare this table of SS to the output of the ANOVA we looked at, at the beginning. The within and between SS values are are exactly the ones it reported.

Now let’s consider the more specific logic of the ANOVA. What would this table look like if the null hypothesis were true?

The between groups SS should be close to zero. If all of the means are the same then the main source of variability would be whatever variability there is within groups. In other words when the null hypothesis is true the within groups SS should tend to be about the same as the total SS.

We’ve seen that we can think of the total SS as coming from two sources (within and between groups) so to answer the question of the ANOVA – Is there at least one difference? – we only need to compare those sources. In other words we should test how much variance is caused by the two sources. That is a fraction.

What to compare it to?

Well we have seen before that chi-squared distribution INSERT LINK is what happens with the sum of the squares of multiple normal distributions. Since one of the assumptions of the ANOVA is that the errors are normally distributed there must be a connection. Indeed we will compare the fraction above to the F-distribution, which is the ratio of two (scaled) chi-squared distributions.

. . . where U₁ and U₂ have degrees of freedom d₁ and d₂ respectively.

In order to scale the F distribution and out description of the data we need to know the degrees of freedom. Within groups there are 2 degrees of freedom and between groups there are 147.

Why are these the degrees of freedom? Degrees of freedom are the number of “free” values in the calculation. Since there are 150 data points and the total SS is fixed the total degrees of freedom is 149, since we could thus determine 150th value using the other 149. Then for the within groups SS is are just 2 degrees of freedom since there are 3 groups we know the within groups SS (same logic). All of the remaining degrees of freedom, then, go to the between groups SS.

This is everything we need to know!

(between.SS/2)/(sum(in.SS)/147)
 1180.161

This is our F-statistic (or f-value) and it says that 1180 times as much variability was between groups as within groups. Give that we are modeling compared to the F-distribution lets look at exactly where we are on the F-distribution (also because its funny) . . .

x <- seq(0,1500,.1) 
y <- df(x,147,2)
plot(y~x,type='l')
arrows(1180,.0125,1180,.1,code=1,angle=30,lwd=2,col='red')
text(1180,.125,'You Are Here',col='red')

The distribution goes off to infinity, of course, we’re just showing a segment of it that helps to highlight just how extreme our result is.

Calculating the exact p-value (the probability of getting a greater result) is just a matter of taking an integral of the probability from 0 to 1180 on this distribution. Doing this precisely is not easy. We can’t estimate “by hand” with summation and even the built in integrate() function that R has lacks the needed precision.

In any even the p-value is extremely low. The aov() function estimates it as less than . . .

. . . which is very small indeed.

To finish up let’s take one last look again at the ANOVA table that R calculated for us. We should understand everything involved.

options(show.signif.stars=F)
mod <- aov(iris$Petal.Length~iris$Species)
summary(mod)
              Df Sum Sq Mean Sq F value Pr(>F)
iris$Species   2  437.1  218.55    1180 <2e-16
Residuals    147   27.2    0.19

We know where the degrees of freedom come from. We understand the sum of squares, the F-value, and the p-value. The only thing we didn’t cover directly was the mean squares. Those are just the SS divided by the degrees of freedom.

Sum of Squares

Let’s look at partitioning the concepts of the sum of squares (or the sum of squared errors) as it is a principle that underlies a number of common statistical tests like the ANOVA, linear regression, and the chi-squared test.

The important principle that underlies the way we use the sum of squares is that if all of the data comes from the same distributions the total sum of squares and the sum of the sum of squares for each group will be the same. This is true but not trivial to prove.

Instead let’s look at it in action.

The sum of squares is defined as . . .

First some random data from a normal distribution . . .

x <- rnorm(2000)

Now we will use some R code to see what happens.

sum.squares <- function(x) {
	sum((x-mean(x))^2)
}

## The SS for each of four partitions
s1 <- sum.squares(x[1:500])
s2 <- sum.squares(x[501:1000])
s3 <- sum.squares(x[1001:1500])
s4 <- sum.squares(x[1501:2000])

## The SS for all of the data.
a <- sum.squares(x)
## Sum of the SS that comes from the partitions.
b <- sum(s1,s2,s3,s4)
a
 504.8449
b
 504.3293
a/b
 1.001022

Yep, the partitioned SS add up to the total SS.

This trait is not unique to the sum of squares. The sum of the absolute errors also has this trait.

sum.abs <- function(x) {
	sum(abs(x-mean(x)))
}

m1 <- sum.abs(x[1:500])
m2 <- sum.abs(x[501:1000])
m3 <- sum.abs(x[1001:1500])
m4 <- sum.abs(x[1501:2000])

a <- sum.abs(x)
b <- sum(m1,m2,m3,m4)
a
 170.3583
b
 170.1077
a/b
 1.001473

Since the absolute value is conceptually simpler than the square it seems like we should just be using the sum of absolutes in the ANOVA but we don’t. Why?

Like many instances of squares in statistics we do this because it makes finding analytic solutions to various problems much easier. The chi-squared distribution exactly describes the distribution of the sum of squares from one or more standard normal distribution.

(Since the standard normal distribution has a mean of zero we don’t have to write the subtraction.)

We can generate its approximate shape easily from some random variables.

e <- rnorm(10000)
f <- rnorm(10000)
g <- rnorm(10000)
s <- e^2+f^2+g^2

d <- data.frame(e,f,g,s)
round(head(d),2)
      e     f     g    s
1  0.58  1.55  0.24 2.79
2  0.19 -0.53 -1.05 1.42
3 -1.27 -0.58 -0.26 2.00
4 -1.02  0.05  1.90 4.66
5  1.08  0.09  0.41 1.35
6 -0.07  0.02 -0.28 0.08

x <- seq(0,10,.1)
y <- dchisq(x,3)
plot(density(s, cut = 0), xlim = c(0,10))
lines(x,y,
	col = 'red',
	lty = 'dashed', lwd = 2)

We already saw the chi-squared distribution once as part of deriving the t-test. We’ll see it again next time when we look at the ANOVA.

The Rank Sum Test

Last time we were looking at the ranks of the differences as part of a paired samples test. This time we will look at the ranks of the raw data. The first thing to do is arrange our data.

## The data
x <- c(3,1,5,8,2)
y <- c(1,2,11,4,10)

## As a single group.
v <- c(x,y)

## Names to keep track of the groups
gr <- c(rep('a',5),rep('b',5))

## Rank the data.
r <- rank(dat)

dat <- data.frame(gr,v,r)
dat
   gr  v    r
1   a  3  5.0
2   a  1  1.5
3   a  5  7.0
4   a  8  8.0
5   a  2  3.5
6   b  1  1.5
7   b  2  3.5
8   b 11 10.0
9   b  4  6.0
10  b 10  9.0

Now we sum the ranks of each group.

tapply(dat$r,dat$gr,sum)
 a  b 
25 30

Group a sums to 25 while group b sums to 30. We don’t look at the distribution of the ranks directly like we did with the Signed Rank test. Instead we will look at the U-distribution.

. . . where n is the number of sample in reach group and R is the sum of ranks for one of the groups. So for group a our sample values of U is . . .

This distribution is defined by the dwilcox() function that comes built in to R.

x <- 0:25
y <- dwilcox(x,5,5)
plot(y~x,type='h')

Like with every other traditional hypothesis test we’ve seen the test itself just involves looking at where we are on the relevant distribution. Again like the signed-rank test the relevant distribution is approaching a normal distribution.

Using a t-Test

In our last post we addressed the question of where exactly the t-distribution used in a t-test comes from.

A t-test is probably the most frequently used statistical test in modern science. It works almost identically to the z-Test (and follows the same concept as the binomial test except) that we are using the more arcane t-distribution to describe a sampling distribution.

Consider the information we have about the weight of baseball players. The weight of those 1033 players is 201 pounds. On the Arizona team, however, the average weight is 208 pounds.

Here is the mean and SD for that team.

mean(tab$weight[tab$team == "ARZ"])
 208.0714
sd(tab$weight[tab$team == "ARZ"])
 24.5386

How do we test to see if this difference is likely to occur by chance than deliberate choice?

Our hypothesis is that the Arizona players are not being picked for their weight so their drawn from a population with a mean of 200 pounds, like everybody else. To find the t-value we subtract the hypothetical mean from sample mean and divide by the sample standard deviation, this is the equation derived last time. We’re attempting to normalize the errors.

arz <- tab$weight[tab$team == "ARZ"]

m.pop <- mean(tab$weight)
m.arz <- mean(arz)
s.arz <- sd(arz)/sqrt(length(arz))

t <- (m.arz-m.pop)/s.arz
t
 1.376252

This is a value that we compare to the t-distribution!

Since there are 28 players on the team we use a distribution with a ν of 27. The density looks like this.

x <- seq(-3,3,0.01)
y <- dt(comb,27)
plot(y~x,type='l',
	main='t-Test with v=27 and t = 1.376')
points(dt(t,27)~t,pch=16,col='red')
arrows(3,.2,1.5,dt(t,27)+.005)
text(2.2,.2,label='you are here')

Like with the binomial test we are looking for the probability of getting a value equal to or greater than the one we observed. The inverse cumulative tells us, for each point, the probability of selecting a greater value.

1-pt(t,27) # pt() is the cumulative t-distribution function, subtracting it from 1 produces the inverse
 0.09002586

We conclude from this that, if Arizona doesn’t tend to pick players with above average weights, there is about a 9% chance of this occurring. That isn’t considered to be impressive evidence so traditionally we would not choose to draw any conclusions here.

But why should you believe me? Surely I’m just a person on the internet who could easily make a mistake while I type. Fortunately R comes with a built in t.test() function.

t.test(arz,mu=m.pop,alternative='greater')
        One Sample t-test

data:  arz
t = 1.3763, df = 27, p-value = 0.09003
alternative hypothesis: true mean is greater than 201.6893
95 percent confidence interval:
 200.1727      Inf
sample estimates:
mean of x 
 208.0714 

There we have it, R confirms my previous claims. The t-statistic is 1.3763, the degrees of freedom are 27, and the p-value is 0.09.

The Z-Test

The z-test, like the binomial test, is a way of testing a hypothesis. It is not a very common form of hypothesis test because it requires us to have a great deal of information we do not usually have but it is an illustrative example that will serve as a stepping stone on the way to the t-test which has more practical applications.

In order to perform a z-test we need to know the the variance of the population that the sample is drawn from. This is not an easy thing to determine in practice.

Many IQ tests are tuned to produce a precise degree of variance when tested on the general population, one of the few somewhat real world examples of an instance where we can use a z-test. Imagine that we are using a test that is designed to have a standard deviation of 10 and a mean of 100. We give this test to 11 people who are supposed to be very clever. Their mean score is 107. The standard error should be:

se <- 10/sqrt(11)
se
 3.015113

Now that we know the standard error we can calculate the z-score in order to draw conclusions about the data we then determine. This is a form of normalization except we are adjusting for variability in the means rather than variability in the data itself. Thanks to the central limit theorem we believe that the mean values of a sample will follow a normal distribution.

z <- (107-100)/se
z
 2.321637

In a literal sense the z-score is how many standard errors from the population mean our sample mean is. This value is now compared to the standard normal distribution (also know as the z-distribution hence the name!) exactly the way we did with the binomial distribution.

1-pnorm(z)
 0.01012624

So there is about a 1% chance of getting a value as large or larger than the one we found and about a 2% chance of getting a value as extreme or more extreme. Generally we would be comfortable concluding that these people are, in fact, better at taking IQ tests than most people.

Standard Error

We’ve used the standard error several times on this blog without going into much detail about it. In simplest possible terms the SE is the range within which we expect a value (typically the mean) to be. Specifically it is the standard deviation of the sample means.

This requires a bit of abstract thought. If you take many samples from a population you will not always get the same mean value. After taking many samples you’ll have a distribution of those means. We are attempting to describe the characteristics of something one step more abstract than the mean. To see a more concrete example refer to the post of efficient estimators.

When we say “the average weight of a baseball player is 200 pounds” we mean that in our sample the average weight is 200 pounds and that we believe this is close to the true average of the population. With the standard error, confidence interval, or credible interval we quantify how close we expect it to be.

Using our baseball player data from a while back, let’s look at how the standard error works in an ideal situation. We know the true mean of the population so let’s take a bunch of random samples and see how often we capture the true value of the mean.

For convenience make the weight its own object:

weight <- tab$weight

Here is the equation that defines the standard error, first in common notation and then as a custom R function.

. . . where s is the sample standard deviation (s² is the sample variance) and n is the sample size.

se <- function(x) {sd(x)/sqrt(length(x))}

Now we use replicate() and sample() to take 1000 samples of 100.

r <- 1000
size <- 100
samps <- replicate(r,sample(weight,size))

Using the apply() function we get the mean and standard error of each sample.

means <- apply(samps,2,mean)
ses <- apply(samps,2,se)

se.h <- means+ses
se.l <- means-ses

Add up all of the instances where the top of the interval is less than the mean or the bottom of the interval is more than the mean. These are the instances where the standard error has missed the true value.

a <- sum(length(se.h[se.h < 201.6893]),length(se.l[se.l > 201.6893]))
1-a/r
 0.709

That’s actually better than we should expect. Keep in mind that the calculation of the standard error relies on us assuming a normal distribution for the population.

So where does the this equation come from?

As you saw before we calculate the standard error as the standard deviation divided by the square root of the sample size or, perhaps more intuitively, the variance divided by the sample size.

We do this because of the Bienayme formula which provides that the sum of the variance of several variables is the same as the variance of the sums of those variables (ie you draw 10 numbers from two populations and add together each pair).

Consider the equation that defines the mean for some data X:

Now imagine a sample of exactly one value. The mean is equal to that value (itself divided by 1) and the variance of those means is exactly the population variance. When we draw a large number of values we can treat our sample as many samples of one (which it is), so then the variance of the sum is the same as the variance of the sample (which is approximately equal to the variance of the population).

This is not a rigorous mathematical proof, of course, the intention is to understand the intuition of why the standard error is the way it is. Personally, I find it comforting to know that the standard error is not produced out of thin air.

Normalization

Here’s a simple but common problem: How do you compare two groups that have different scales?

Imagine we are giving assessment tests to several school classes but all of them have been designed differently. Test A ranges from 0 to 100, in increment of a tenth of a point. Test B only offers scores between 0 and 12. Finally Test C is scored between 200 and 800 for arcane reasons known only to the designers. Here is the data we collected, they can all be copied directly into R.

a <- c(69.6, 74.8, 62.7, 54.2, 66.8,
	48.7, 48.7, 67.8, 69.1, 85.1,
	51.2, 54.6, 53.9, 56.4, 51.5,
	73.5, 53.4, 76.1, 60.5, 62.7,
	54.9, 66.8, 54.3, 49.2, 57.3,
	61.3, 61.8, 70.4, 51.1, 53.4)
b <- c(3, 5, 5, 6, 7,
	4, 6, 8, 5, 4,
	5, 5, 6, 6, 5,
	4, 5, 7, 6, 6,
	2, 5, 5, 0, 6,
	5, 4, 5, 6, 4)
c <- c(560, 529, 593, 607, 627,
	597, 544, 531, 584, 510,
	420, 543, 577, 623, 531,
	598, 508, 555, 642, 490,
	596, 626, 597, 514, 602,
	569, 635, 551, 518, 617)

group <- c(rep('a',30),rep('b',30),rep('c',30))

These aren’t easy to make comparisons between the three classes because the tests have such radically different scales. We can look at the descriptive statistics to see how unhelpful the raw data is for purposes of comparison.

mean(a); mean(b); mean(c)
[1] 60.72
[1] 5
[1] 566.46

sd(a); sd(b); sd(c)
[1] 9.46
[1] 1.53
[1] 51.03

Personally I think it’s much funnier to plot the distributions.

dat <- data.frame(group = group, score = c(a,b,c))

p <- ggplot(dat,aes(x=score,color=group))
p + geom_density(size=2) + 
	xlab('score')

Yeah, not helpful.

One method of normalization is simply to report the percentage score, this is called non-dimensional normalization since it makes no assumptions about the data. To do this we subtract the minimum possible score and divide by the maximum possible score.

aa <- (a-0)/100
bb <- (b-0)/12
cc <- (c-200)/800

dat <- data.frame(group = group, score = c(aa,bb,cc))

p <- ggplot(dat,aes(x=score,color=group))
p + geom_density(size=2) + 
	xlab('normalized score') + 
	scale_x_continuous(limits=c(0,1))

Now that they are all on a common scale we can visually compare them.

Notice that the shape of the distributions has not changed (you can see this most clearly with group a). Now we can make some actual meaningful comparisons.

mean(aa); mean(bb); mean(cc)
[1] 0.607
[1] 0.416
[1] 0.458
sd(aa); sd(bb); sd(cc)
[1] 0.094
[1] 0.127
[1] 0.063

The most popular form of dimensional normalization is the z-score or standard score which forces the data into having certain characteristics of a standard normal distribution. Creating a z-score is done by transforming the data so that mean equals 0 and the standard deviation equals 1. This is actually pretty easy to do. For each data point we subtract the mean and divide by the standard deviation.

# We make a function of our own to do it quickly.
normalize <- function(x) {
	(x-mean(x))/sd(x)
}
aa <- normalize(a)
bb <- normalize(b)
cc <- normalize(c)

This isn’t as immediately intuitive as calculating a percentage but it does have some advantages. One immediately advantage is that if a z-score is less than 0 that means the score is worse than average for the group and if the z-score is more than 0 it is better than average.

dat <- data.frame(group = group, score = c(aa,bb,cc))

p <- ggplot(dat,aes(x=score,color=group))
p + geom_density(size=2) + 
	xlab('normalized score')

Z-scores are used to compute p-values as part of the Z-test. We will use the Z-test as a lead in to the t-test.

Normalization is also the term used for taking a distribution and ensuring that it integrates or sums to 1, thus becoming a probability distribution. In fact this process is so important that several probability distributions are named after the function that normalizes them like the binomial distribution, the gamma distribution, and the beta distribution.

Central Limit Theorem – Again

A lot of decisions made in statistics rely on the central limit theorem. While the CLT is a bit abstract it is important enough that time should be taken to understand it. It goes like this:

The characteristics of independent samples from a population are approximately normally distributed.

It is important to note that this refers to the distribution of samples, not of the data itself (while many processes are normally distributed this is essentially a side effect of the above statement). This fact about samples is very useful because, as we saw when we looked briefly at the normal distribution, this means it is rare for sample values to dramatically from the population.

For example, the mean height of an American is about 162 centimeters. Even though there are three hundred million citizens it should be difficult to make a random sample of fifty people which has mean height of 100 centimeters.

What’s interesting and significant is that the CLT works with most distributions, you can estimate the mean even of strangely shaped data. Indeed this is so common that distributions that are exceptions, like the Cauchy distribution are considered “pathological”.

Before we continue let’s look at samples from a few different distributions.

# A population of ten thousand for the gamma, uniform, normal, and cauchy distributions.
gam <- rgamma(10000,1)
uni <- runif(10000)
nor <- rnorm(10000)
cau <- rcauchy(10000)

# The true mean of each population.
mg <- mean(gam)
mu <- mean(uni)
mn <- mean(nor)
mc <- mean(cau)

# We take a sample of fifty from each population one thousand times with a quick function.
samp.means <- function(x,rep=1000,n=50) {
	density(colMeans(replicate(1000,sample(x,n))))
}

pgam <- samp.means(gam)
puni <- samp.means(uni)
pnor <- samp.means(nor)
pcau <- samp.means(cau)

First we’ll visualize the shape of the distributions.

Now we visualize the shape of sample means, a vertical line shows the location of the true mean (the value we want to get).

For the first three the sample means stay close to the true mean even though they are very different in shape. For the Cauchy the samples have means that are all over the place, although the density happens to be highest near the true mean. Fortunately pathological distributions like the Cauchy are extremely rare in practice.

We talked about this before but we’re taking a second look at it again as part of a series that will lead to the t-test. There are actually a number of different central limit theorems. For example, one of the central limit theorems tells us that for normally distributed variables . . .

Which is to say that the sample mean, xbar, for a sample of size n, is distributed as a normal distribution with a mean of μ and a variance of σ² divided by the sample size. The Greek letters indicate characteristics of the population.

A formal proof of the behavior of samples from a normal distribution is available from PennState.

The fact that the central limit theorems are true is an extremely important result because they tell us a) that a sample will tend to be centered on the population mean and that b) it will tend to be relatively close. Moreover the

It is easy to demonstrate that the CLT is true but there is no immediately intuitive way to explain why the CLT is true. Nonetheless let’s use R to see this occur visually by looking at two trivial cases.

First imagine what happens with a sample of 1. The result of many samples will just be that we draw an identical distribution, one point at a time.

Now if we consider a taking a sample of 2 it is less obvious what will happen but we can write some code for an animation that will give us some idea.

x <- NULL
for(i in 1:50) {
	r <- rnorm(2)
	x[i] <- mean(r)
	h <- hist(x,plot=F,
		breaks=seq(-4,4,.25))
	
	comb <- seq(-4,4,.1)
	ncur <- dnorm(comb)

	title <- paste0('image',i,'.svg')
	svg(title)
	par(mfrow=c(2,1))
	plot(ncur~comb,type='l',xlab='')
	points(dnorm(r)~r,col='red')
	plot(h$counts~h$mids,type='h',
		xlim=c(-4,4),ylim=c(0,10),
		xlab='Mean',ylab='Count',
		lwd=3,col='red')
	dev.off()
}

We choose two values, compute the mean, and record it. Then repeat that process many times to slowly build up a distribution of means.

Weird Facts from MTG JSON – Art

Welcome back to my irregular series Weird Facts from MTG JSON, using data made available by Robert Shultz on his site.

It is a truth universally acknowledged that the Magic creative team tends to give cards a dominant color scheme that corresponds to their Color. How can we test this this hypothesis?

The mtgimage site provides easily available images of the art for every card. There are far too many cards to practically apply this method to the whole history of the game so we’re going to take a look at a limited section of them. Since the core sets have no particular theme I expect they’ll be less influenced by the artistic tone of a given block.

Between them the last several core sets have more than one thousand cards. We will adapt some code from the is.R() blog on tumblr to extract the images.

library(jpeg)
library(RCurl)
library(MASS)

a <- AllCards[AllCards$set == 'M10',]
b <- AllCards[AllCards$set == 'M11',]
c <- AllCards[AllCards$set == 'M12',]
d <- AllCards[AllCards$set == 'M13',]
e <- AllCards[AllCards$set == 'M14',]
f <- AllCards[AllCards$set == 'M15',]

l <- rbind(a,b,c,d,e,f)

w <- l[l$color == "W",]
u <- l[l$color == "U",]
b <- l[l$color == "B",]
r <- l[l$color == "R",]
g <- l[l$color == "G",]

l <- rbind(w,u,b,r,g)

code <- l$ID

urls <- paste("http://mtgimage.com/multiverseid/",codes,"-crop.jpg", sep="")

Running the actual extraction takes a while but we only have to do it once.

jpglist <- list()
for (i in 1:length(urls)) {
	jpglist[[i]] <- readJPEG(getURLContent(urls[i]))
}

This next complicated bit of code comes again from the is.R() blog. You can read more about it there. The idea is that is the color information from the raster image is can be averaged in order to produce coordinates in color space.

meanRGB <- t(sapply(jpglist,function(ll) {
	apply(ll[,,-4],3,mean)
}

cardDistance <- dist(meanRGB)
cardDistance[cardDistance <= 0] <- 1e-10
MDS <- isoMDS(cardDistance)$points

Bind the color and name of each card to its position in color space then save the data so we don’t have to run the loop in the future.

col <- as.character(l$color)
name <- l$name
posCol <- data.frame(MDS,col,name)

save(posCol,file="posCol.Rdata")

There is now a file in R’s working directory called posCol.Rdata which you can load directly into R with the load() function.

Then we make a simple scatter plot and make all the colors line up with appropriate Colors. The goal here is simply to be able to identify clustering if there is any. In order to deal with the fact that the cards are ordered by color we’ll randomize them.

posCol <- posCol[sample(nrow(posCol)),]

p <- ggplot(posCol,aes(x=X1,y=X2,color=col))
p + geom_point(size=2) + 
	scale_color_manual(values=c('black','green','red','blue','white'))

You can see some distinct regions of dominance in the image. Red and Blue are are mostly separate, but White shares space with them. Green shares a lot of space with Black.

We can go a bit deeper into this analysis, rather than just rely on what I conclude by eyeballing the scatterplot. The mean position for each color is easy to calculate (if not terribly robust) and we can then compute a distance matrix.

x <- with(posCol,tapply(X1,col,mean))
y <- with(posCol,tapply(X2,col,mean))

mean.pos <- data.frame(x,y)
round(dist(x,y),3)
      B     G     R     U
G 0.082                  
R 0.154 0.094            
U 0.135 0.084 0.161      
W 0.196 0.115 0.123 0.101

The matrix suggests that Green and Black (or maybe Green and Blue) are the most similar Colors in terms of the color palate used for them. By far the most dissimilar are Black and White, although both Red and Blue and Red and Black are close follow ups. By a couple of different metrics it is apparent that Black has the least variability in color while Blue has the most.

We can do a better job of visually checking the variability of the colors positions as well.

We can also use ggplot2 to draw contour lines with the geom_density2d() layer that estimates the density in two dimensions. This makes seeing a middle for each plot much easier.

This makes the incredible similarity in color palate between Green and Black the most apparent. Perhaps surprising for enemy colors.